Construct a function whose reflection in the line of y=x is itself. State the symmetries of the function.

Question

asked Jan 11, 2019 73.7k views

1 Answer

Demaunt · Answer 1 · 2019-01-18T19:27:05+0000

ANSWER TO PART A

The mapping for the reflection in the line
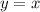y=x , is given by

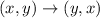$(x,y)\rightarrow (y,x)$ .

That is the coordinates swap position .

The only way we can construct a function
f(x) , such that;

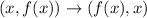$(x, f(x))\rightarrow (f(x),x)$ are equal is when

f(x)=x .

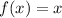So that when
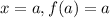x=a, f(a)=a .

The mapping then becomes

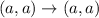$(a,a)\rightarrow (a,a)$ .

Therefore the function,
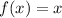f(x)=x is the function whose reflection in the line

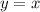y=x is itself.

ANSWER TO PART B

The function is symmetrical with respect to the origin. That is to say the function is an odd function.

A function is symmetric with respect to the origin, if it satisfies the condition,

f(-x)=-f(x)

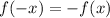
For instance,

f(a)=a

f(-a)=-a

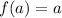
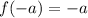
Since

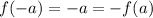
f(-a)=-a=-f(a)

We say the function is symmetric with respect to the origin.