Let us assume total number of students were surveyed = x.
1/4 of x students preferred red = 1/4 x.
1/8 of of x students preferred blue = 1/8 x
Remaining students = (x - 1/4 x - 1/8 x)
3/5 of the remaining students chose green that is 3/5 of (x - 1/4 x - 1/8 x).
15 students preferred green.
So, we can setup an equation:
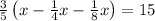
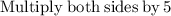
![[tex]5\cdot (3)/(5)\left(x-(1)/(4)x-(1)/(8)x\right)=15\cdot \:5](https://img.qammunity.org/2019/formulas/mathematics/high-school/sppwe5aid2rdvf33k2zd159j4w6eglssdt.png) [/tex]
[/tex]
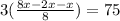
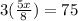
Dividing both sides by 3.

Multiplying both sides by 8, we get
5x = 200.
Dividing both sides by 5, we get
x= 40.
Therefore, 40 students were surveyed.