For a function to begin to qualify as differentiable, it would need to be continuous, and to that end you would require that
 is such that
is such that
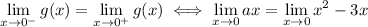
Obviously, both limits are 0, so
 is indeed continuous at
is indeed continuous at
 .
.
Now, for
 to be differentiable everywhere, its derivative
to be differentiable everywhere, its derivative
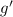 must be continuous over its domain. So take the derivative, noting that we can't really say anything about the endpoints of the given intervals:
must be continuous over its domain. So take the derivative, noting that we can't really say anything about the endpoints of the given intervals:
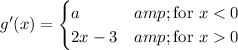
and at this time, we don't know what's going on at
 , so we omit that case. We want
, so we omit that case. We want
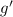 to be continuous, so we require that
to be continuous, so we require that

from which it follows that
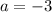 .
.