Question

For the function f x equals square root x ^ 3 - x, State the condition that must be satisfied for the FX to be Define. Then, solve the condition to determine the domain

Answer 1

Domain:
`[-1,0]\cup [1,\infty )`

Explanation:

Since we know that a square root function is not defined for negative numbers. In order our function to be defined values inside radical must be greater than or equal to zero.

Our function will be defined when
`x^(3) -x\geq 0`

`x(x^(2) -1)\geq 0`

`x(x-1)(x+1)\geq 0`

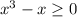
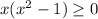
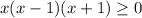
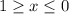`1\geq x\leq 0` or
`x\geq1`

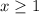
Now we will use number line method of solving inequalities to check whether our answer is right or not.

Let us try -2, -1/2, 1/2 and 2 to check which conditions meet our criteria.

`-2^(3) --2\geq 0\\-6\leq 0`

`((-1 )/(2)) ^(3) -((-1)/(2)) \geq0`

`(-1)/(8) +(1)/(2) \geq 0\\(3)/(8) \geq 0`

`((1 )/(2)) ^(3) -(1)/(2) \geq0`

`(1)/(8) -(4)/(8) \leq 0`

`2^(3) -2\geq 0\\6\geq 0`

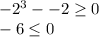
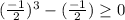
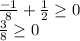
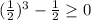
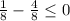
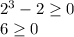
Therefore, we can see that our function is defined when
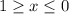`1\geq x\leq 0` or
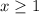`x\geq1` and domain of f(x) is
`[-1,0]\cup [1,\infty )`.