A friction force of 280 N exists between a cart and the path. If the force of reaction is 766 N, what is the minimum action force needed to set the cart in motion?

Question

asked Sep 17, 2019 86.2k views

1 Answer

Tricasse · Answer 1 · 2019-09-21T23:54:25+0000

force of friction on the cart is given as

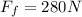
F_f = 280 N

here we also know the reaction force due to surface

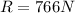
R = 766 N

so we can say reaction force is given as

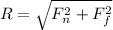
R = √(F_n^2 + F_f^2)

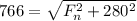
766 = √(F_n^2 + 280^2)

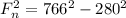
F_n^2 = 766^2 - 280^2

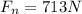
F_n = 713 N

now by force balance we will say

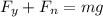
F_y + F_n = mg

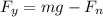
F_y = mg - F_n

F_x = F_f

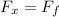
also we know that

$F_f = \mu * F_n$

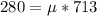
$280 = \mu * 713$

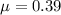
$\mu = 0.39$

now minimum force required to set this into motion

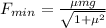
$F_(min) = (\mu mg)/(√(1 + \mu^2))$

here we know that

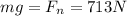
mg = F_n = 713 N

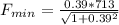
F_(min) = (0.39* 713)/(√(1 + 0.39^2))

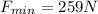
F_(min) = 259 N

So it will require 259 N minimum force to move it