Question

Determine the multiplicity of the roots of the function k(x) = x(x + 2)3(x + 4)2(x − 5)4. 0, -2, -4, 5

Answer 1

0 has multiplicity 1

−2 has multiplicity 3

−4 has multiplicity 2

5 has multiplicity 4

Answer 2

The polynomial function
`k(x)=x(x+2)^3(x+4)^2(x-5)^4`

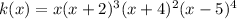
To determine the multiplicity of 0, -2, -4, 5.

The multiplicity of a root is the number of times the root appears.

First find the root of the equation, set the function equals to zero.

`x(x+2)^3(x+4)^2(x-5)^4=0`

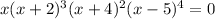
therefore, the root of this function are, x=0,-2, -4, 5

To find the multiplicity of the roots:

A factor of x would have a root at x=0 with multiplicity of 1

similarly, x=-2 with multiplicity of 3

x=-4 with multiplicity of 2

x=5 with multiplicity of 4.