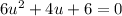Question

Write 6(x – 5)4 + 4(x – 5)2 + 6 = 0 in the form of a quadratic by using substitution.

A. 6u2 + 4u + 6 = 0, where u = x – 5
B. 6u2 + 4u + 6 = 0, where u = (x – 5)2
C. 6u4 + 4u + 6 = 0, where u = x – 5
D.6u4 + 4u + 6 = 0, where u = (x – 5)2

The answer is  B. 6u2 + 4u + 6 = 0, where u = (x – 5)2 

Answer 1

B

Explanation:

Answer 2

We are given the equation:

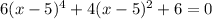`6(x-5)^(4)+4(x-5)^(2)+6=0`..........(1)

Now we have to write it in quadratic form using substitution.

The general form of quadratic equation is given by:

`ax^(2)+bx+c=0`

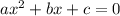
So let us say

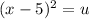`(x-5)^(2)=u`.......(2)

Plugging the value of (x-5)² from equation (2) in (1),

`6u^(2)+4u+6=0`

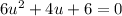
Answer : Option B.
`6u^(2)+4u+6=0`