Question

Type the correct answer in the box. Use numerals instead of words. If necessary, use / for the fraction bar.

The product of (3 + 2i) and a complex number is (17 + 7i).

The complex number is ?

Answer 1

37+55i

Explanation:

The product of (3 + 2i) and a complex number is (17 + 7i) is expressed as shown below:

(3+2i)(17+7i)

Expanding the bracket,

= 51+21i+34i+14i²

= 51+55i+14i²

Note that in complex numbers i² = -1

Substituting this into the result, we have:

= 51+55i+14(-1)

= 51+55i-14

= 37+55i

The product of both complex number is 37+55i

Answer 2

The product of (3 + 2i) and a complex number is (17 + 7i)

The product of (3 + 2i) and a complex number is (17 + 7i).

Let the complex number be a + ib

Product means we multiply

So (3+2i) * (a + ib) = (17+7i)

WE need to find a+ ib

Divie by 3 + 2i on both sides

a + ib = (17+7i) / (3+2i)

To divide multiply by the conjugate (3-2i)

`a + ib = (( 17+7i)*(3-2i))/((3+2i)(3-2i))`

`a + ib = (((17*3+7*2)+(7*3-17*2)i)/(3^2-2^2)`

`a + ib = (((65)+(-13)i)/(13)`

`a+ib = (65)/(13) - (13)/(13)`

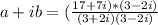
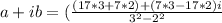
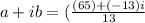
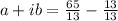
a+ib = 5 - i

The required complex number is 5 - i