Question

Barbara drives between Miami, Florida, and West Palm Beach, Florida. She drives 50 mi in clear weather and then encounters a thunderstorm for the last 16 mi. She drives 18 mi slower through the thunderstorm than she does in clear weather. If the total time for the trip is 1.5 hr, determine her speed driving in nice weather and her speed driving in the thunderstorm.

Answer 1

Drive Faster!

Explanation:

Answer 2

Her speed driving in nice weather is 50 mph and in thunderstorm is 32 mph.

Explanation:

Barbara drives 50 miles in clear weather and then encounters a thunderstorm for the last 16 miles.

Suppose, her speed in nice weather is
`x` mph.

As she drives 18 mph slower through the thunderstorm than she does in clear weather, so her speed in thunderstorm will be:
`(x-18) mph`

We know that,
`Time = (Distance)/(Speed)`

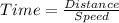
So, the time of driving in clear weather
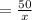`=(50)/(x)` hours

and the time of driving in thunderstorm
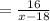`=(16)/(x-18)` hours.

Given that, the total time for the trip is 1.5 hours. So, the equation will be......

`(50)/(x)+ (16)/(x-18)=1.5 \\ \\ (50x-900+16x)/(x(x-18))=1.5\\ \\ (66x-900)/(x(x-18))=1.5 \\ \\ 1.5x(x-18)=66x-900\\ \\ 1.5x^2-27x=66x-900\\ \\ 1.5x^2-93x+900=0\\ \\ 1.5(x^2 -62x+600)=0\\ \\ x^2 -62x+600=0\\ \\ (x-50)(x-12)=0`

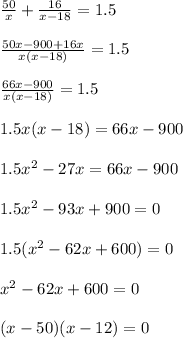
Using zero-product property.........

`x-50=0\\ x=50\\ \\ and\\ \\ x-12=0\\ x=12`

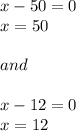
We need to ignore
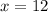`x=12` here, otherwise the speed in thunderstorm will become negative.

So, her speed driving in nice weather is 50 mph and her speed driving in thunderstorm is (50-18) = 32 mph