Answer:
(a)
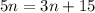
(b)
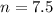
Solution is not viable
Explanation:
(a)
Total number of red ping pong balls
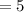
Total number of red ping pong balls
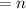
Now, probability of an event
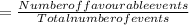
Then, theprobability of randomly choosing a blue ping pong ball is
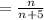
Given that this probability is
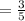
Thus, we have that,

(b)
Solving, the above equation,
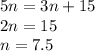
This solution is not viable as, number of ping pong ball must be an integer and not a decimal number.