Question

ain ABC, AB=x, because=y, and CA=2x. A similarity transformation with a scale factor of 0.5 Maps ABC to MNO, such that vertices M,N and O correspond to A,B,C respectively. If OM=5, what is AB?

Answer 1

Explanation:

Answer 2

We are given: Triangle ABC sides, AB = x, BC = y and CA = 2x.

Another triangle MNO whose vertices M,N and O correspond to A,B,C respectively.

Therefore, AB corresponding to sides MN , BC corresponding to sides NO and CA corresponding to sides OM.

Also, we are given " A similarity transformation with a scale factor of 0.5 Maps ABC to MNO".

That means triangle ABC is dilated by a factor of 0.5.

Each side of the triangle MNO is 0.5 times(half) of Triangle ABC.

We could also say that each side of Triangle ABC is two times of sides of triangle MNO.

We are given side OM = 5 units.

CA = Times of OM = 2 * 5 = 10 units.

CA = 2x = 10 units or 2x=10.

Dividing both sides by 2, we get

`(2x)/(2)=(10)/(2)`

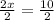
x=5.

AB = x.

Therefore, AB = 5 units.