To find the distance, you would use the distance formula, which is:
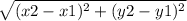
But, in this case, both of the x values are 13, meaning we can cancel out the x values (or just subtract y₁ from y₂, to get the distance ):

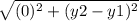
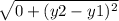
Because of this, we only need to find the distance between y₁ and y₂. Plug in the -6 and 12:
 Plug in both y terms.
Plug in both y terms.
 Simplify as much as possible.
Simplify as much as possible.
= 18 The √ and the ² cancel out.
Therefore, the distance between (13, -6) and (13, 12) is 18.
Hope this helps! :)
EDIT: all the subscripts and most of the exponents showed up incorrectly. should be fixed now.