Question

What is the pre-image of vertex A' if the rule that created the image is ry-axis(x, y) → (–x, y)?

Answer 1

It is given that image of any point (x,y) is (-x,y).

It is the case of reflection of a point through Y - axis.

So , Image of point (x,y) is (-x,y).

it's pre-image will be Point A whose coordinate is (x,y).

Answer 2

Answer: Preimage of A' is A (x,y).

Explanation:

Suppose we have given a point A' (-x,y) and let
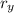`r_y` be the rotation transformation with center of rotation at origin(0,0) such that

`r_y (x,y) =(-x,y) \\`

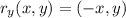
Now in rotation transformation of any point about y axis i.e.(
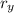`r_y`) it produces the reflected image by changing the polarity of x abscissa only and not of y. Therefore, by applying rotation transformation about y axis on image A'(-x,y) gives the pre-image of (-x,y) = (x,y) [which is the reflection of A'].

For example :- let P (1,2) be any point then after rotation transformation about y axis it will become P'(-1,2).