Question

Find the domain for the rational function f of x equals quantity x minus 1 end quantity divided by quantity x plus 3 end quantity.

(−∞, 1) (1, ∞)
(−∞, −1) (−1, ∞)
(−∞, 3) (3, ∞)
(−∞, −3) (−3, ∞)

Answer 1

`\mathrm{Domain\:of\:}\:(x-1)/(x+3)\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x<-3\quad \mathrm{or}\quad \:x>-3\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:-3\right)\cup \left(-3,\:\infty \:\right)\end{bmatrix}`

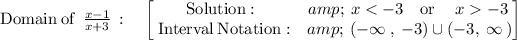
Therefore, the 4th option i.e. (−∞, −3) (−3, ∞) is the correct answer.

Explanation:

Given the expression

`f\left(x\right)=(x-1)/(x+3)`

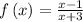
We know that the domain is the set of all the input or argument values for which is the function is real and defined.

From the given expression, we need to make sure the denominator of a rational function can be anything but 0, because 0 would make the function undefined.

Thus, we need to find undefined points such as:

x+3 = 0

x = -3

Therefore, the function domain must be:

x < -3 or x > -3

In other words,

`\mathrm{Domain\:of\:}\:(x-1)/(x+3)\::\quad \begin{bmatrix}\mathrm{Solution:}\:&\:x<-3\quad \mathrm{or}\quad \:x>-3\:\\ \:\mathrm{Interval\:Notation:}&\:\left(-\infty \:,\:-3\right)\cup \left(-3,\:\infty \:\right)\end{bmatrix}`

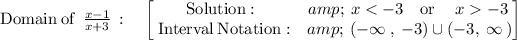
Therefore, the 4th option i.e. (−∞, −3) (−3, ∞) is the correct answer.