Question

The area of a circle is 100 π.what is the lenght of the side of a tegular hexagon inscribed in a circle.

Answer 1

This logic, geometric logic at that.

First find the radius of the circle.


`area = \pi {r}^(2) \\`
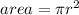
We find the radius by a little algebraic manipulation.


`area = \pi {r}^(2) \\ \sqrt{ (area)/(\pi) } = r \\ \sqrt{ (100\pi)/(\pi) } = r \\ radius = 10`

Answer:

The height of the hexagon is 10 units (whatever the units are, every measurement needs units). All the sides of a polygon are equal, and it's a regular hexagon, which is a polygon. It's simple thinking, mostly people get into trouble when they over think it