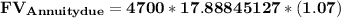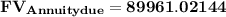Question

Dwayne invests $4,700 in a savings account at the beginning of each of the next twelve years. if his opportunity cost rate is 7 percent compounded annually, how much will his investment be worth after the last annuity payment is made? use the equation method to calculate the worth of the investment. (round your answer to two decimal places.)​

Answer 1

Answer: Dwayne's investment will be worth $89,961.02 after the last annuity payment is made.

Since Dwayne contributes $4700 at the beginning of each year, we need to calculate the future value of an annuity due.

We use this formula for our calculations:

`\mathbf{FV _(Annuity due) = PMT * \left [ ((1+r)^(n)-1)/(r) \right ]*(1+r)}`

Substituting the values we get,

`\mathbf{FV _(Annuity due) = 4700 * \left [ ((1+0.7)^(12)-1)/(0.07) \right ]*(1+0.07)}`

`\mathbf{FV _(Annuity due) = 4700 * \left [ \frac{2.252191589}-1}{0.07} \right ]*(1.07)}`

`\mathbf{FV _(Annuity due) = 4700 * \left [ \frac{1.252191589}}{0.07} \right ]*(1.07)}`

`\mathbf{FV _(Annuity due) = 4700 * 17.88845127 *(1.07)}`

`\mathbf{FV _(Annuity due) = 89961.02144}`