Question

Vera wants to graph a line that passes through (0, 2) and has a slope of . Which points could Vera use to graph the line? Check all that apply. (–3, 0) (–2, –3) (2, 5) (3, 4) (6, 6)

Answer 1

A,D, AND E i just took the test.

Answer 2

we have

1) The line passes through
`(0,2)`

2) The slope is equal to
`(2)/(3)`

we know that

If a point lies on the graph of the line, then the point must satisfy the equation of the line

Step 1

Find the equation of the line

we know that

the equation of the line in point-slope form is equal to

`y-y1=m*(x-x1)`

we have

`(x1,y1)=(0,2)`

`m=(2)/(3)`

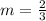
substitute in the equation

`y-2=(2)/(3)*(x-0)`

`y=(2)/(3)x+2`

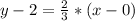
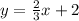
we will proceed to verify each of the points to determine the solution of the problem

If a point lies on the graph of the line, then the point must satisfy the equation of the line and the equation will be true for the point

Step 2

Point
`(-3,0)`

Substitute the value of x and y in the equation of the line

`0=(2)/(3)*(-3)+2`

`0=-2+2`

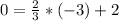
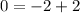
`0=0` -------> is true

therefore

the point
`(-3,0)` lies on the line

Step 3

Point
`(-2,-3)`

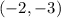
Substitute the value of x and y in the equation of the line

`-3=(2)/(3)*(-2)+2`

`-3=-(4)/(3)+2`

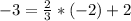
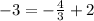
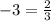`-3=(2)/(3)` ------> is false

therefore

the point
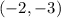`(-2,-3)` not lies on the line

Step 4

Point
`(2,5)`

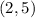
Substitute the value of x and y in the equation of the line

`5=(2)/(3)*(2)+2`

`5=(4)/(3)+2`

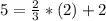
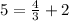
`5=(10)/(3)` ------> is false

therefore

the point
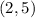`(2,5)` not lies on the line

Step 5

Point
`(3,4)`

Substitute the value of x and y in the equation of the line

`4=(2)/(3)*(3)+2`

`4=2+2`

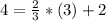
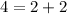
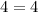`4=4` ------> is True

therefore

the point
`(3,4)` lies on the line

Step 6

Point
`(6,6)`

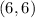
Substitute the value of x and y in the equation of the line

`6=(2)/(3)*(6)+2`

`6=4+2`

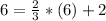
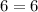`6=6` ------> is True

therefore

the point
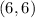`(6,6)` lies on the line

therefore

the answer is

Vera could use the points

the point
`(-3,0)`

the point
`(3,4)`

the point
`(6,6)`

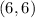
using a graphing tool

see the attached figure to better understand the problem