Question

How are the solutions for |x + 4| < –2 and |x + 4| < 2 different? A. They are not different, because the inequality is an absolute value. B. The first inequality has no solution because absolute value cannot be negative. C. For one, the solution is between two numbers. For the other, the solution is outside of the two numbers. D. For one the solution is a range of positive numbers, for the other, the solution is a range of negative numbers.

Answer 1

Answer: B. is correct

Answer 2

The answer is B.

The absolute value is the "positive version" of a number. So, the absolute value does nothing to positive numbers, and switches the sign of negative numbers. Here are some examples:

`|4| = 4,\quad |-3|=3,\quad\left|(-3)/(2)\right|=(3)/(2),\ldots`

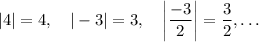
So, as you can see, the result of an absolute value can't be negative, and as such, it can't be less than a negative number.