The object will hit the ground in 4.3 s.
The formula used for the object thrown by Chay is:
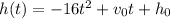
According to the problem,
Initial velocity
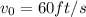
Initial height
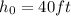
Therefore,

When the object hits the ground h(t) becomes 0.
Thus,
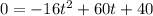
Dividing both sides by 4 we get;
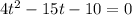
Solving by applying quadratic formula;
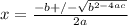
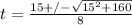
t=4.3s