Question

Ardem collected data from a class survey. He then randomly selected samples of five responses to generate four samples.

Survey Data

Sample 1

4

5

2

4

3

Sample 2

2

2

6

5

7

Sample 3

4

6

3

4

1

Sample 4

5

2

4

3

6


Using his four samples, between what two numbers will Ardem’s actual population mean lie?

1 and 6

2 and 5

3.6 and 4.4

4.0 and 4.4

Answer 1

3.6 and 4.4

Explanation:

Answer 2

Solution: The sample mean of sample 1 is:

`\bar{x}=(4+5+2+4+3)/(5)= (18)/(5)=3.6`

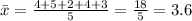
The sample mean of sample 2 is:

`\bar{x}=(2+2+6+5+7)/(5)= (22)/(5)=4.4`

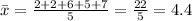
The sample mean of sample 3 is:

`\bar{x}=(4+6+3+4+1)/(5)= (18)/(5)=3.6`

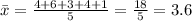
The sample mean of sample 4 is:

`\bar{x}=(5+2+4+3+6)/(5)= (20)/(5)=4`

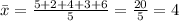
The minimum sample mean of the four sample means is 3.6 and maximum sample mean of the four sample means is 4.4.

Therefore, using his four samples, between 3.6 and 4.4 will Ardem's actual population mean lie.

Hence the option 3.6 and 4.4 is correct