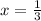Question

How do you know if 2x+3y=9xy is linear or nonlinear.

Answer 1

There are several characteristics that define a linear function:

1) They are of the form
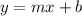`y = mx + b`, where m and b are real constants, or they can also have the form
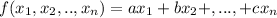`f (x_(1) , x_(2), .., x_(n)) = ax_(1) + bx_(2) +, ..., + cx_(n)` if the function is of several variables. Where a, b, c are real numbers.

2) The degree of the variable x is always equal to 1 or 0. That is, if there is an expression of the form
`x^(-1)` or
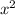`x ^ {2}`, the function is not linear.

3) Your domain is all real numbers

4) The graph of its function in the xy plane is always a straight line.

Analyzing the aforementioned equation:

The function
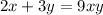`2x + 3y = 9xy` does not have the form described, since it has a multiplication of two variables (
`9xy`).

The graph of its function in the xy plane is a hyperbola

Your domain is not all real numbers, because the function is not defined for
`x=(1)/(3)`

Answer 2

We are given equation 2x+3y=9xy.

A linear equation is a equation that has maximum degree of the equation as 1.

Degree is the maximum power(exponent) of the variables.

If two variables are being multiplied together in a term, we can find power of the that term by adding powers of those variables.

In the given equation, on the left side we have two terms 2x and 3y, each opf the variable x, and y has power 1 and right side of the eqaution we have term 9xy. There x and y variables are being multiplied together.

So, the total power of the term would be 1+1=2.

So, the degree of the given equation would be 2.

Because degree of the given equation is not 1. Therefore, given equation is not a linear eqaution and it is a non-linear equation.