Question

The area of the rhombus is 540 cm2; the length of one of its diagonals is 4.5 dm. What is the distance between the point of intersection of the diagonals and the side of the rhombus?

Answer 1

Area of rhombus =
`(xy)/(2)`

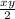
where x and y are diagonals.

Given length of one diagonal is 4.5 dm

So, let x= 4.5dm

1 dm = 10 cm

4.5dm= 45cm

area =
`(xy)/(2)`

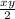
so,
`540 = (45y)/(2)`

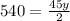
y = 24 cm

The two diagonals are x= 45cm and y = 24cm

Since diagonals bisect each other, we get 22.5cm and 12cm

Using right triangle formula

`(1)/(r^(2) ) = (1)/(22.5^(2)) + (1)/(12^(2))`

`(1)/(r^(2) ) =(12^(2)+22.5^(2))/(22.5^(2)*12^(2))`

`r^(2) = (22.5^(2) *12^(2))/(12^(2)+22.5^(2))`

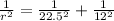
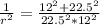
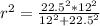
r = 10.588cm

Distance of center to the side =
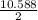`(10.588)/(2)` = 5.294 cm