The largest area that can be enclosed to the nearest square meter will be 348613 m²
Step-by-step explanation
Suppose, the length and width of the rectangular plot are
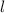 and
and
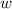 respectively.
respectively.
The farmer does not fence the side along the highway. Lets assume, the farmer does not fence across one length side. So, the total fence needed

Given that, the length of the fence is 1670 meters. So, the equation will be.....
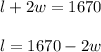
Now, the area of the plot.....
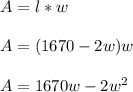
Taking derivative on both sides of the above equation in respect of
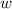 , we will get.....
, we will get.....
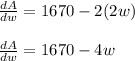
Now
 will be maximum when
will be maximum when
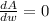 . So....
. So....
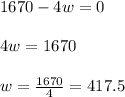
Thus, the area will be:
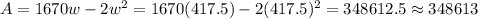
So, the largest area that can be enclosed to the nearest square meter will be 348613 m²