Question

Describe the continuity of the graphed function. Select all that apply.

Answer 1

we know that

Any function f(x) is continuous at x=a only if

`\lim_(x \to a-) f(x) = \lim_(x \to a+) f(x)=f(a)`

We can see that this curve is smooth everywhere except at x=-1

so, we will check continuity at x=-1

Left limit is:

`\lim_(x \to -1-) f(x) = 0`

Right limit is:

`\lim_(x \to -1+) f(x) = 1`

Functional value:

`f(-1)= 1`

we can see that left limit is not equal to right limit

so, limit does not exist

so, this function is discontinuous at x=-1

Since, limit does not exists

so, there will be jump discontinuity at x=-1

so, option-C........Answer

Answer 2

The answer is A and C

Explanation:

You could tell by seeing the plot of a function that it has a discontinuity if you can't trace ir without lifting your pen from the sheet, as you can see, you have to lift your pen in x = -1.

you can make it by math too.

if you remember the concept a function f(x) is continuous at x = a if

`\lim_(x \to \ a^(+)) f(x) =  \lim_(x \to \a^(-) ) f(x) = f(a)\\`

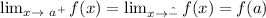
as you can see by looking at x = -1

`\lim_(x \to \-1^(-)) f(x) =  0\\ \lim_(x \to \-1^(+)) f(x) = 1\\`

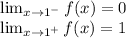
as you can see the lateral limits are different so int means that the function is not continuous.

But there's another right answer

the first option A says that the function is continuous at x = -4

let's proof it again

`\lim_(x \to \-4^(-)) f(x) = 3\\ \lim_(x \to \-4^(+)) f(x) = 3`

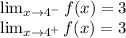
in this case both limits are equal, but this is not reason enough, we have to proof that the function at x = -4 exists. Does it?, let's check

F(-4) = 3 by looking at the graph so the lateral limits are equal and the function in this value exist so the function is continuous at x = -4

Correct answer is A and C