Question

Please help me with this!

Choose the right system for each equation(picture)
Picture one: Inconsistent, consistent, or equivalent?
Picture two: Inconsistent, consistent, or equivalent?
picture three: Inconsistent, consistent, or equivalent?
picture four: Inconsistent, consistent, or equivalent?
picture five: Inconsistent, consistent, or equivalent?

Answer 1

pic 1: equivalent

pic 2 : consistent

pic 3: consistent

pic 4: inconsistent

pic 5: equivalent.

number 6 incase you have it y=3x-2, 3x-y=4 :inconsistent

Explanation:

consistent means they share a point, equivalent is when they have infinite or many touching points so basically the same line. And inconsistent means no sharing points so two different lines.

Answer 2

1. The first equation is - 2x + 5y = 0

Second equation is
`y = (2)/(5) x`

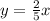
5y = 2x

- 2x + 5y = 0

Hence, the two equations are equivalent.

2.
`a_(1) = 2, a_(2) = - 2`

`b_(1) = -1,  b_(2) = -1`

`(a_(1) )/(a_(2)) =(2)/(-2) = -1`

`(b_(1) )/(b_(2)) = (-1)/(-1)  = 1`

`(a_(1) )/(a_(2)) \\eq (b_(1) )/(b_(2))`

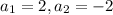
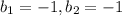
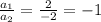
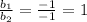
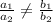
Hence, the equations are consistent.

3.
`a_(1) = 4, a_(2) = 6`

`b_(1) = -1, b_(2) = -1`

`(a_(1) )/(a_(2)) =(4)/(6) = (2 )/(3)`

`(b_(1) )/(b_(2)) = (-1)/(-1) = 1`

`(a_(1) )/(a_(2)) \\eq (b_(1) )/(b_(2))`

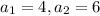
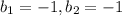
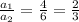
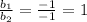
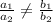
Hence, the equations are consistent.

4. Equations can be re-arranged as:

x + y - 4 = 0 and

x + y + 6 = 0

`a_(1) = 1, a_(2) = 1`

`b_(1) = 1, b_(2) = 1`

`c_(1) = -4, c_(2) = 6`

`(a_(1) )/(a_(2)) =(1)/(1) = 1`

`(b_(1) )/(b_(2)) =(1)/(1) = 1`

`(c_(1) )/(c_(2)) =(-4)/(6) = (-2)/(3)`

`(a_(1) )/(a_(2)) = (b_(1) )/(b_(2)) \\eq (c_(1) )/(c_(2))`

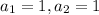
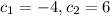
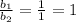
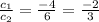
Hence, the equations are inconsistent.

5. If we multiply the first equation by 4, we will get,

2y = -4x + 20 which is the second equation.

Hence, the equations are equivalent.