Question

A certain ball is dropped from a height of x feet. It always bounces up to 2/3 x feet. Suppose the ball is dropped from 10 feet and stopped exactly when it touches the ground after the 30th bounce. What is the total distance traveled by the ball? Express your answer in exponential notation

Answer 1

The total distance traveled by the ball is
`60(1-((2)/(3))^(31))-10`

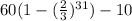
Explanation:

It is given that a certain ball is dropped from a height of x feet. It always bounces up to 2/3 x feet. So, it will form a G.P..

The ball is dropped from 10 feet. So first term of the GP is 10. The second term of the GP is

`a_2=(2)/(3)(10)`

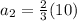
The required GP is

`10,10(2)/(3),10((2)/(3))^2,....`

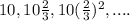
Common ratio of the GP is

`r=(2)/(3)`

The ball stopped exactly when it touches the ground after the 30th bounce.

Since ball stopped after 30th bounce, so we need to find the sum of 31 terms.

The total distance traveled by the ball is

`\text{Total distance}=2* S_(31)-10`

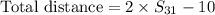
The formula for sum of n terms of a GP is

`S_n=(a(1-r^n)/((1-r))`

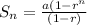
where, a is first term and r is common ratio.

`S_(31)=(10(1-((2)/(3))^(31)))/((1-((2)/(3))))`

`S_(31)=(10(1-((2)/(3))^(31)))/((1)/(3))`

`S_(31)=30(1-((2)/(3))^(31))`

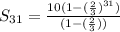
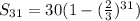
The total distance traveled by the ball is

`\text{Total distance}=2* 30(1-((2)/(3))^(31))-10`

`\text{Total distance}=60(1-((2)/(3))^(31))-10`

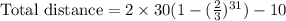
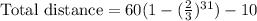
Therefore the total distance traveled by the ball is
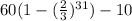`60(1-((2)/(3))^(31))-10`.

Answer 2

Given that if a ball is dropped from x feet, it bounces up to 2/3 x feet.

And the ball is dropped from 10 feet, that is x=10 feet,

So,before the first bounce it travels 10 feet distance.

Between first and second bounce it travels
`(2)/(3)* 10 + (2)/(3) * 10 = 20*((2)/(3))`

Between second and third bounce, it travels
`20*((2)/(3))^(2)`

Between third and fourth bounce, it travels
`20*((2)/(3)) ^(3)`

Like that between 29th and 30th bounce, it travels
`20*((2)/(3) )^(29)`

Hence total distance traveled is

`10+20*((2)/(3) )+20*((2)/(3))^(2) + 20*((2)/(3)) ^(3)+......+20*((2)/(3))^(29)`

=
`10+20[((2)/(3)) +((2)/(3)) ^(2) +((2)/(3)) ^(3) +.....+((2)/(3) )^(29) ]`

=
`10+20[((2)/(3)*(1-((2)/(3))^(29))  )/(1-(2)/(3) )]`

= 10+20*2*(1-
`((2)/(3)) ^(29)`)

= 49.9997 feet ≈ 50 feet approximately.