Question

A colony of 200 weasels on a remote island are suffering from a new disease. Let w(t) be the number of sick weasels at time t. Suppose that 30 weasels are sick initially and the disease is spreading at a rate proportional to the product of the time elapsed and the square root of the number of sick weasels. Give the mathematical model (ivp) for w.

Answer 1

Given that w(t) is the number of sick weasels at time t.

And there are 30 sick weasels initially.

That is at t=0, w is 30. Else we can write that as w(0)=30.

And also given that disease is spreading at a rate proportional to product of time elapsed and square root of the number of sick weasels.

That is dw/dt is proportional to t*w.

Let k be the proportionality constant.

Hence differential equation is
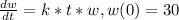`(dw)/(dt) = k*t*w, w(0)=30` as initial condition.