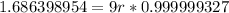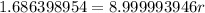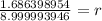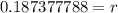Answer: The continuous growth rate of koalas is 18.7%.
We use the formula for continuous growth to find the rate of growth. The formula is:
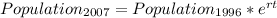
Substituting the values we get,
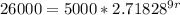
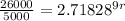
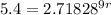
We can solve this equation further by taking the normal log of both sides of the equation.