Question

If we represent the sun as a volleyball (diameter = 65 cm), how far away would we find earth in this model? Note: the sun's actual diameter is 1.4×1091.4×109 meters, and earth is 1.5×10111.5×1011 meters from the sun.

Answer 1

We are supposed to find the distance between sun and earth of the given model, where sun's diameter is given to be 65 cm.

Let the model's distance between Earth and Sun be x.

To find the model's distance between sun and earth we can set an equation of the given information.

`\frac{\text{Diameter in the model}}{\text{Distance in the model}}=\frac{\text{Actual diameter}}{\text{Actual distance}}`

`(65)/(x)=(1.4* 10^(9))/(1.5* 10^(11))`

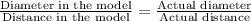
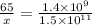
Now let us solve for x.

`x=(65\cdot (1.5* 10^(11)))/(1.4* 10^(9))`

`=(65* 1.5* 10^(11))/(1.4* 10^(9))`

`=(97.5* 10^(11))/(1.4* 10^(9))`

`=(97.5* 10^((11-9)))/(1.4)`

`=(97.5* 10^(2))/(1.4) =(9750)/(1.4)`

`=6964.2857`

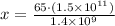
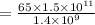
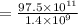
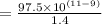
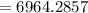
Therefore, model's distance between Earth and Sun is 6964.29 centimeters.