A cone is placed inside a cylinder as shown. The radius of the cone is half the radius of the cylinder. The height of the cone is equal to the radius of the cylinder. What is th…

Question

asked Dec 19, 2019 92.0k views

2 Answers

Niclas Sahlin · Answer 1 · 2019-12-20T11:08:43+0000

Answer:

(1/12) Pi r^3 option C on plato

Explanation:

r = radius of the cylinder

V = (1/3)Pi c^2 h for a cone.

and c = r/2 and h = u

so Volume of the cone is (1/12) Pi r^3

Marcellorvalle · Answer 2 · 2019-12-23T17:00:19+0000

we can use

volume of cone formula

$V=(1)/(3) \pi r'^2 h'$

where

r' is radius of cone

h' is height of cone

we are given

The radius of the cone is half the radius of the cylinder

so,

r'=(r)/(2)

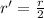
The height of the cone is equal to the radius of the cylinder

so,

h'=r

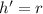
now, we can plug values into formula

we get

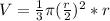
$V=(1)/(3) \pi ((r)/(2))^2*r$

we can simplify it

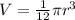
$V=(1)/(12) \pi r^3$

so, option-C.........Answer