Question

Polygon ABCD is dilated, rotated, and translated to form polygon A′B′C′D′. The endpoints of AB are at (0, -7) and (8, 8), and the endpoints of AB are at (6, -6) and (2, 1.5). What is the scale factor of the dilation?

Answer 1

Rotation and translation are rigid transformations, they don't change figure sizes. Dilation change figure sizes increasing or decreasing them by scale factor.

First, find AB and A'B' by the formula:

`AB=√((x_B-x_A)^2+(y_B-y_A)^2)= √((8-0)^2+(8-(-7))^2)=√(8^2+15^2)=√(64+225)=√(289)=17,\\ \\A'B'=\sqrt{(x_(B')-x_(A'))^2+(y_(B')-y_(A'))^2}= √((2-6)^2+(1.5-(-6))^2)=√(4^2+7.5^2)=√(16+56.25)=√(72.25)=8.5.`

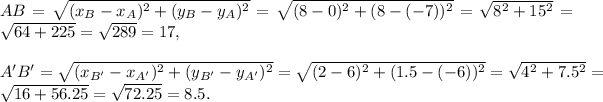
As you can see AB=2A'B'. This means that the segment AB was decreased twice to form segment A'B'. Then the scale factor is 1/2.