Find the values of x and y for 3x + 2iy = 6 + 10i

Question

asked Mar 11, 2019 119k views

2 Answers

Dean Swiatek · Answer 1 · 2019-03-13T14:28:14+0000

Answer: The required values are x = 2 and y = 5.

Step-by-step explanation: We are given to find the values of x and y from the following equation :

3x+2iy=6+10i~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)

To find the values of x and y from the given equation, we need to compare the real and imaginary parts of the equation.

After comparing the real and imaginary parts from both sides of equation (i), we get

$3x=6\\\\\Rightarrow x=(6)/(3)\\\\\Rightarrow x=2$

and

$2y=10\\\\\Rightarrow y=(10)/(2)\\\\\Rightarrow y=5.$

Thus, the required values are x = 2 and y = 5.

Niko B · Answer 2 · 2019-03-15T18:33:09+0000

In this question, the given equation is

3x + 2yi = 6 + 10i

To solve for x and y, we have to compare both sides, and on doing so, we will get

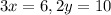
3x=6, 2y=10

Now we need to isolate x and y, by getting rid of 3 and 2 , that is with x and y respectively .

x=2, y=5

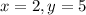
So for the given equation to be true, the values of x and y are 2 and 5 respectively .