Given:In quadrilateral WXYZ , `bar(WY)` and `bar(XZ)` bisect each other at point A. Prove: Quadrilateral WXYZ is a parallelogram.

Question

asked Nov 18, 2019 12.1k views

2 Answers

Annchit R Sarma · Answer 1 · 2019-11-24T13:06:20+0000

Consider the quadrilateral WXYZ, it is given that the diagonals bisect each other that means ZO = OX and WO = OY.

To prove: The quadrilateral WXYZ is a parallelogram.

Proof:

Consider the triangles ZOY and WOX,

Here, OZ = OX

WO = OY

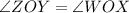$\angle ZOY = \angle WOX$ (Vertically opposite angles)

Therefore,
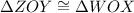$\Delta ZOY\cong \Delta WOX$ By SAS criteria

Therefore, ZY = WX and
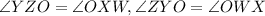$\angle YZO = \angle OXW , \angle ZYO = \angle OWX$ (By Cpct)

Consider the triangles ZOW and YOX,

Here, OZ = OX

WO = OY

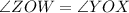$\angle ZOW = \angle YOX$ (Vertically opposite angles)

Therefore,
$\Delta ZOW\cong \Delta YOX$ By SAS criteria

Therefore, ZW = YX and
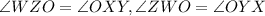$\angle WZO = \angle OXY , \angle ZWO = \angle OYX$ (By Cpct)

Therefore, now we get ZY=WX , ZW=YX that is opposite sides of the given quadrilateral are equal.

Since,
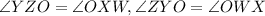
$\angle YZO = \angle OXW , \angle ZYO = \angle OWX$

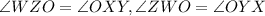
$\angle WZO = \angle OXY , \angle ZWO = \angle OYX$

Consider
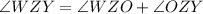
$\angle WZY = \angle WZO + \angle OZY$

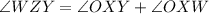
$\angle WZY = \angle OXY + \angle OXW$

$\angle WZY = \angle WXY$

Now, consider
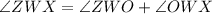
$\angle ZWX = \angle ZWO + \angle OWX$

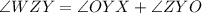
$\angle WZY = \angle OYX + \angle ZYO$

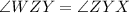
$\angle WZY = \angle ZYX$

Hence, opposite angles of the given quadrilateral are equal.

Hence, the given quadrilateral is a parallelogram.