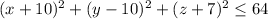Question

Write down an (in)equality which describes the solid ball of radius 8 centered at (−10,10,−7). it should have a form like x2 y2 (z−2)2−4>

Answer 1

The equation of a sphere (I mean only the surface) is

`(x-x_0)^2 + (y-y_0)^2 + (z-z_0)^2 = r^2`

where
`(x_0,y_0,z_0)` is the center of its sphere, and
`r` is its radius. This equation simply menas "consider the points who are exactly
`r` units away from the center".

So, if instead of the sphere surface we want the solid ball, we need to consider all the points whose distance from the center is less than or equal to the radius. So, the equation becomes

`(x+10)^2 + (y-10)^2 + (z+7)^2 \leq 64`

Answer 2

A sphere centered at (h, j, k) with radius r has equation

... (x-h)² + (y-j)² + (z-k)² = r²

A solid ball with the same center will have any radius up to r. Your ball has equation

... (x +10)² +(y -10)² +(z +7)² ≤ 64