Question

The ray ‾ ⇀gj is the angle bisector of ∠fgh and m∠fgh = 75° how do you find ∠fgj

Answer 1

For a better understanding of the solution/explanation given here please go through the diagram in the file attached.

By definition, an angle bisector is a ray that divides an angle into two congruent angles.

In our question we have been given that GJ is the ray that is the angle bisector and that has been shown in the diagram.

Now, since,
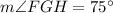`m\angle FGH=75^(\circ)`, therefore, the ray
`\underset{GJ}{\rightarrow}` will divide the original angle
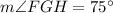`m\angle FGH=75^(\circ)` into two congruent angles,
`\angle GJH` and
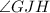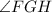`\angle FGH`. Since, the division is equal, the values of both these angles will be half of the original angle. Thus, we will have:

`\angle FGJ=\angle HGJ=(75^(\circ))/(2)=37.5^(\circ)`

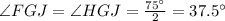
Thus, the required value of
`\angle FGJ=37.5^(\circ)`