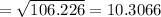Question

Ten people at a party decide to compare ages. Five people are 30 years old, three are 32, one is 31, and one is 65. Given the ages of the ten people, to the nearest tenth, determine the average of their ages and the standard deviation. A. The mean age of the ten people at a party is ____ B. The standard deviation is: ____

Answer 1

A. The mean age of the ten people at a party is: 34.2

B. The standard deviation is: 10.3066

Explanation:

We are given a information about the age of ten people as:

Age(in years) Number of people

30 5

32 3

31 1

65 1

Hence, the mean of the age is calculated as:

`Mean(x')=(30* 5+32* 2+31+65)/(10)\\\\\\Mean(x')=(342)/(10)\\\\\\Mean(x')=34.2`

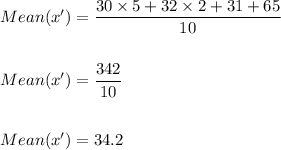
Now, we calculate the standard deviation in the following steps:

x x-x' (x-x')²

30 -4.2 17.64

30 -4.2 17.64

30 -4.2 17.64

30 -4.2 17.64

30 -4.2 17.64

32 -2.2 5.06

32 -2.2 5.06

32 -2.2 5.06

31 -3.2 10.24

65 30.8 948.64

∑ (x-x')²= 1062.26

Variance=∑ (x-x')²/10=106.226

Hence, standard deviation is the square root of variance.

standard deviation is:

`=√(106.226)=10.3066`

Answer 2

The mean age is 34.2. I'm working on the standard deviation right now, I'll comment on this post when I figure it out.