The length that results in the maximum area is 39 feet.
Step-by-step explanation
Lets assume, length of the rectangle is
 feet and width of the rectangle is
feet and width of the rectangle is
 feet.
feet.
As the length and width must add up to 78 feet, so the equation will be...

Solving equation (1) for y :
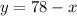
Now the area of the rectangle,
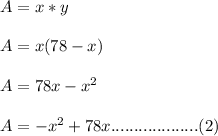
 will be maximum when
will be maximum when
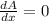
Now taking derivative of equation(2) with respect to
 ......
......

If
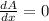 , then
, then
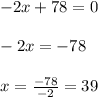
If
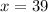 , then
, then
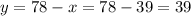
So, both length and width will be 39 feet for getting maximum area.
The length that results in the maximum area is 39 feet.