We simply have to plug the values
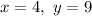 in all inequalities, and see if the result is true for all inequalities in the system:
in all inequalities, and see if the result is true for all inequalities in the system:
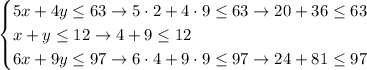
So, the system becomes
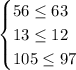
So, only the first inequality is true, and thus the point is not in the feasible set of this system of inequalities