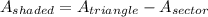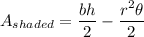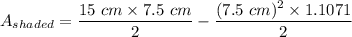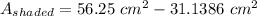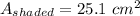Question

Please help me !!! Tmr i got my exam tomorrow!!!

Answer 1

QP is a tangent to the circle at P. A tangent to a circle at a point on the circle is perpendicular to the radius of the circle drawn to that point on the circle. That makes angle P a right angle, so triangle QPO is a right triangle. OQ is the hypotenuse of the right triangle, and QP and OP are the legs. For angle O, QP is the opposite leg, and OP is the adjacent leg. The trig function that relates the opposite leg to the adjacent leg is the tangent. QP = 2OP = 2(7.5 cm) = 15 cm.

Part (a)

`\tan O = (opp)/(adj)`

`\tan \theta = (15~cm)/(7.5~cm)`

`\tan \theta = 2`

`\theta = \tan^(-1) 2 = 1.1071~radians`

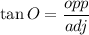
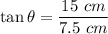
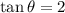
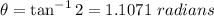
Part (b)

The area of the shaded portion of the triangle is the area of the triangle minus the area of the sector of the circle.

`A_(shaded) = A_(triangle) - A_(sector)`

`A_(shaded) = (bh)/(2) - (\theta)/(2 \pi)\pi r^2`

`A_(shaded) = (bh)/(2) - (r^2 \theta)/(2)`

`A_(shaded) = (15~cm * 7.5 ~cm)/(2) - ((7.5~cm)^2 * 1.1071)/(2)`

`A_(shaded) = 56.25~cm^2 - 31.1386~cm^2`

`A_(shaded) = 25.1~cm^2`