Question

Verify that -5, 1/2, and 3/4 are the zeroes of the cubic polynomial 4x^3+20x^2+2x-3. Also verify the relationship between the zeroes and the coefficient

Answer 1

we have been asked to verify that -5, 1/2, and 3/4 are the zeroes of the cubic polynomial
`4x^3+20x^2+2x-3`

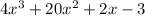
To verify that whether the given values are zeros or not we will substitute the values in the given Polynomial, if it will returns zero, it mean that value is Zero of the polynomial. But if it return any thing other than zeros it mean that value is not the zero of the polynomial.

Let
`f(x)=4x^3+20x^2+2x-3\\\\\text{when x=-5}\\\\f(-5)=4(-5)^3+20(-5)^2+2(-5)-3=-13\\\\\text{when x=}(1)/(2)\\`

`f( (1)/(2) ) = 4 ( (1)/(2) )^3+20((1)/(2))^2+2((1)/(2))-3=(7)/(2)\\\\`

`\text{when x=}(3)/(4)\\\\`

`f( (3)/(4) ) = 4 ( (3)/(4) )^3+20((3)/(4))^2+2((3)/(4))-3=(183)/(16)\\`

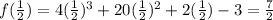
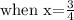
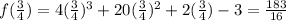
Hence -5, 1/2, and 3/4 are not the zeroes of the given Polynomial.

Since sum of roots
`=(-b)/(a)= (-20)/(4)=-5\\`

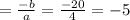
But
`-5+(1)/(2)+(3)/(4)= (-15)/(4)\\eq-5`

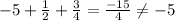
Hence we do not find any relation between the coefficients and zeros.

Anyway if the given values doesn't represents the zeros then those given values will not have any relation with the coefficients of the p[polynomial.