The given sequence is 2, 6, 18, 54, ...
Notice that this is a geometric sequence because here we have equal common ratio.
So, common ratio :

=
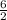
= 3
The formula for general term of a geometric sequence is,

Where, first term: a_{1} =2
Next step is to plug in these values in the above equation to get the formula for the given sequence.
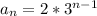
Hence, the correct choice is A.