If
 and
and
 are odd positive integers, they are one more than a non-negative even number, i.e. there exists
are odd positive integers, they are one more than a non-negative even number, i.e. there exists
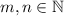 such that
such that
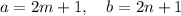
So, the first expression become
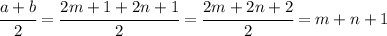
Similarly, we have
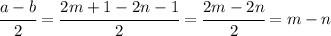
Now, the parity of these expressions depend on those of
 and
and
 . We have four cases:
. We have four cases:
If both m and n are even:
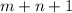 is odd, since
is odd, since
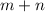 is even, while
is even, while
 is even
is even
If one of the two is odd and the other is even:
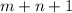 is even, since
is even, since
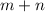 is odd, while
is odd, while
 is odd
is odd
If both are odd:
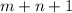 is odd, since
is odd, since
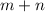 is even, while
is even, while
 is even
is even
So, in all cases, one between (a+b)/2 and (a-b)/2 is odd, and the other is even.