Question

Plzz help me solve questions 15 and 16...!!

Answer 1

15.

We have right triangles, with the ladder the hypotenuse of both and the wall the opposite side of both.

Call the ladder length h.

Against the wall we have the opposite of alpha the taller one:

`q = h \sin \alpha - h \sin \beta`

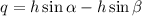
On the ground adjacent to beta is the longer one

`p = h \cos \beta - h \cos \alpha`

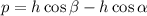
Dividing

`\frac p q = ( h \cos \beta - h \cos \alpha )/(h \sin \alpha - h \sin \beta) = ( \cos \beta -\cos \alpha )/(\sin \alpha - \sin \beta) \quad\checkmark`

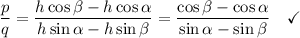
16.

Again I'm too lazy to draw the figure but you should.

Let's call y the height of the tower and x the distance from the observation point on the ground to the base of the tower.

`\tan 60^\circ = \frac y x`

`\tan 30^\circ = (y - 40)/(x)`

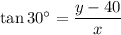
Since
`\sin 30 =\cos 60 = \frac 1 2 \textrm{ and } \cos 30 = \sin 60 = √(3)/2`

`\tan 60^\circ = √(3) = y/x`

`\tan 30^\circ = 1/√(3) = (y-40)/x`

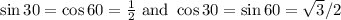
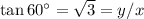
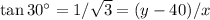
Dividing,

`√(3)/ (1/√(3)) = (y/x) / ((y-40)/x)`

`3 = y/(y-40)`

`3y - 120 = y`

`2y = 120`

`y = 60`

`x = y/√(3) = 60(√(3)/3) = 20 √(3)`

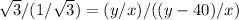
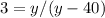
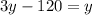
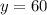
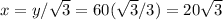
Answer: Height 60 meters, distance 20√3 meters