Question

Let f(x) = 8x3 − 22x2 − 4 and g(x) = 4x − 3. Find f of x over g of x.

2x2 − 4x − 3 − 13 over quantity 4x minus 3
2x2 − 4x − 3 − quantity of 4 x minus 3 over 13
2x2 − 7x − 1
2x2 − 7x − 5 + quantity of x minus 4 over quantity of 4 x minus 3

Answer 1

Given that
`f(x)=8x^3-22x^2-4` and
`g(x)=4x-3`

Question says to find f of x over g of x which simply means divide value of f(x) by value of g(x)

Dividing them gives:

`(f(x))/(g(x))=(8x^3-22x^2-4)/(4x-3)`

Denominator is already in factored form which can't divide numerator means it can't be simplified more.

Hence final answer is
`(f(x))/(g(x))=(8x^3-22x^2-4)/(4x-3)`.

other part of question is not clear so i will skip them.

Answer 2

The correct answer is the first one.

Explanation:

We have the functions
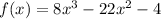`f(x) = 8x^3-22x^2-4` and
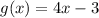`g(x) = 4x-3`. Then, the fraction is

`(f(x))/(g(x)) = (8x^3-22x^2-4)/(4x-3)`.

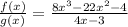If we want to give a ‘‘simplified’’ expression for this quotient we must do a a division of polynomials. The algorithm is the analogue for the division of integers. Attached there is an image of the procedure.

After the completion of the division algorithm we obtain

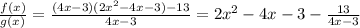`(f(x))/(g(x)) = ((4x-3)(2x^2-4x-3)-13)/(4x-3) = 2x^2-4x-3 - (13)/(4x-3)`.