Question

As John walks 50 ft towards a chimney, the angle of elevation from his eye to the top of the chimney changes from 30° to 45°. Identify the height of the chimney rounded to the nearest foot.

80 ft

50 ft

68 ft
96 ft

Answer 1

Observe the image attached. In this triangle ABD, AD is the height of the chimney. Let BC be the distance traveled by John towards the chimney. As we can observe in the image how the angle of elevation changes from
`30^(\circ)` to
`45^(\circ)`.

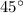In the triangle ABD,

`\tan 30^(\circ) = (AD)/(BD)`

`\tan 30^(\circ)=(h)/(50+CD)`

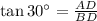
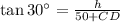
Let the distance CD be x meters.

`\tan 30^(\circ)=(h)/(50+x)`

`(1)/(√(3)) = (h)/(50+x)`

`50+x=h√(3)`

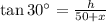
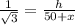
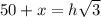
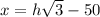`x=h√(3)-50` (Equation 1)

In the triangle ACD,

`\tan 45\dot{^(\circ)} = (AD)/(CD)`

`1=(h)/(x)`

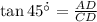
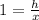
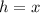`h=x` (Equation 2)

Substituting the value of x from equation 2 in the equation 1,

`h=h√(3)-50`

`50=h√(3)-h`

`h=(50)/(√(3)-1)`

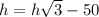
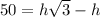
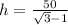
h= 68.3 feet.