Question

How can the Pythagorean Identity be used to find sin θ, cos θ, or tan θ and the quadrant location of the angle?

Answer 1

First lets see the pythagorean identities

`sin^2 \Theta + cos^2 \Theta =1`

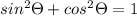
So if we have to solve for sin theta , first we move cos theta to left side and then take square root to both sides, that is

`sin^2 \Theta = 1-cos^2 \Theta => sin \theta = \pm √(1-cos^2 \Theta)`

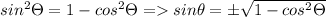
Now we need to check the sign of sin theta

First we have to remember the sign of sin, cos , tan in the quadrants. In first quadrant , all are positive. In second quadrant, only sin and cosine are positive. In third quadrant , only tan and cot are positive and in the last quadrant , only cos and sec are positive.

So if theta is in second quadrant, then we have to positive sign but if theta is in third or fourth quadrant, then we have to use negative sign .