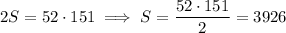Question

50+51+52+...+101=...
Can you help me? I do not understand

Answer 1

Suppose

`S=50+51+52+\cdots+100+101`

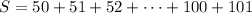
At the same time, we can write

`S^*=101+100+99+\cdots+51+50`

Note that
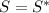`S=S^*` (just reverse the sum). Let's pair the first terms of
`S` and
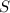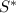`S^*`, and the second, and the third, and so on:

`S+S^*=(50+101)+(51+100)+(52+99)+\cdots+(100+51)+(101+50)`

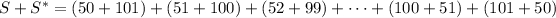
Now, each grouped term in the sum on the right side adds to 151. There are 52 grouped terms on that same side (because there are 50 numbers in the range of integers 51-100, plus 50 and 101), which menas

`S+S^*=52\cdot151`

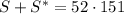
But
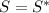`S=S^*`, as we pointed out, so

`2S=52\cdot151\implies S=\frac{52\cdot151}2=3926`