Given the equation
y=
![\[log_2(x)\]](https://img.qammunity.org/2019/formulas/mathematics/high-school/pa2q6co0w6o5gfg0mswwug2alloasesloq.png)
{(1/2,?), (1, ?), (2, ?), (4,?), (8,?), (16, ?)}
Lets start with (1/2, ?)
Ordered pair is (x,y)
In (1/2, ?) , x=1/2 and we need to find out y
y=
![\[log_2(x)\]](https://img.qammunity.org/2019/formulas/mathematics/high-school/pa2q6co0w6o5gfg0mswwug2alloasesloq.png)
Plug in 1/2 for x, y=
![\[log_2(1/2)\]](https://img.qammunity.org/2019/formulas/mathematics/high-school/1ihl0i1tsw44j3co570nj6gflle6kgz8zm.png) =
=
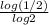 = -1
= -1
we do the same for all ordered pairs
(1, ?)
Plug in 1 for x, y=
![\[log_2(1)\]](https://img.qammunity.org/2019/formulas/mathematics/high-school/p5lgx4ujylevv11ipd93ufiwk2re8joxft.png) =
=
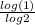 = 0
= 0
(2, ?)
Plug in 2 for x, y=
![\[log_2(2)\]](https://img.qammunity.org/2019/formulas/mathematics/high-school/pdrv24pwbrca2w0bz47ec4q1mpmzxexnzk.png) =
=
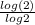 = 1
= 1
(4, ?)
Plug in 4 for x, y=
![\[log_2(1)\]](https://img.qammunity.org/2019/formulas/mathematics/high-school/p5lgx4ujylevv11ipd93ufiwk2re8joxft.png) =
=
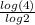 = 2
= 2
(8, ?)
Plug in 8 for x, y=
![\[log_2(8)\]](https://img.qammunity.org/2019/formulas/mathematics/high-school/2id05q77v5z3fxmk7ldkluhfibcurlydms.png) =
=
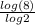 = 3
= 3
(16, ?)
Plug in 16 for x, y=
![\[log_2(16)\]](https://img.qammunity.org/2019/formulas/mathematics/high-school/zkq0s6kke30azspq1ve6dj2fyj9ijly2sc.png) =
=
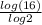 = 4
= 4
Ordered pairs are
{(1/2,-1), (1, 0), (2, 1), (4,2), (8,3), (16, 4)}