Question

Derive the equation of the parabola with a focus at (2,-1) and a directrix of y=-1/2

Answer 1

Answer: -(x-2)^2-3/4

Answer 2

keeping in mind that the vertex is "p" distance from either the focus or directrix, that means is half-way between both, check the picture below.

from -1 to -1/2 the distance is just 1/2 and half of that is 1/4.

now, if we go down from the directrix which is at -1/2, by 1/4 of a unit, we'll end up at

`\bf \cfrac{1}{2}+\cfrac{1}{4}\implies \cfrac{2+1}{4}\implies \cfrac{3}{4}\qquad \qquad vertex~\left(\stackrel{h}{2}~,~\stackrel{k}{-(3)/(4)} \right)`

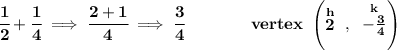
the distance "p" is obviously 1/4, however, since the parabola is opening downwards, is negative, therefore -1/4.

`\bf \textit{parabola vertex form with focus point distance}\\\\\begin{array}{llll}4p(x- h)=(y- k)^2\\\\\boxed{4p(y- k)=(x- h)^2}\end{array}\qquad \begin{array}{llll}vertex\ ( h, k)\\\\ p=\textit{distance from vertex to }\\\qquad \textit{ focus or directrix}\end{array}\\\\-------------------------------`

`\bf \begin{cases}h=2\\k=-(3)/(4)\\\\p=-(1)/(4)\end{cases}\implies 4\left( -(1)/(4) \right)\left[y- \left( -(3)/(4) \right) \right]=(x-2)^2\\\\\\-1\left( y+(3)/(4) \right)=(x-2)^2\implies y+\cfrac{3}{4} =-(x-2)^2\\\\\\y=-(x-2)^2-\cfrac{3}{4}`