Question

What is the equation of the following graph in vertex form? (3 points) parabolic function going down from the left through the point zero comma five and turning at the point two comma one and continuing up towards infinity

Answer 1

The correct answer is A, "y = (x - 2)² + 1."

Explanation:

I just completed the test and got it right.

Answer 2

We have vertex form for parabola equation as

`Y = a(X-h)^2 + k`

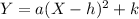
where (h,k) is the vertex.

As the turning point given here is (2,1) so thats the vertex.

On comparing (2,1) with (h,k), we can see

h = 2, k = 1

Plugging 2 in h place and 1 in k place in

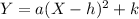`Y = a(X-h)^2 + k` we get

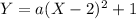`Y =a(X-2)^2 + 1` ------------------------ (1)

Now we need to find value of a.

For that we will use point (0,5) given on parabola.

On comparing (0,5) with point (X,Y) we get X = 0, Y = 5

so plug 0 in X place and 5 in Y place in equation (1)

`Y = a(X-2)^2 + 1`

`5 = a(0 -2)^2 + 1`

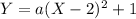
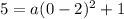
Simplify and solve for a as shown

`5 = a(-2)^2 + 1`

`5 = a(4) + 1`

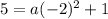
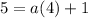
5 -1 = a(4) + 1 - 1

4 = a(4)

`(4)/(4) = (a(4))/(4)`

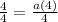
1 = a

Now plug 1 in a place in equation (1) as shown

`Y = 1(X-2)^2 + 1`

`Y = (X-2)^2 + 1`

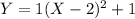
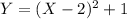
So thats the vertex equation of parabola and final answer.